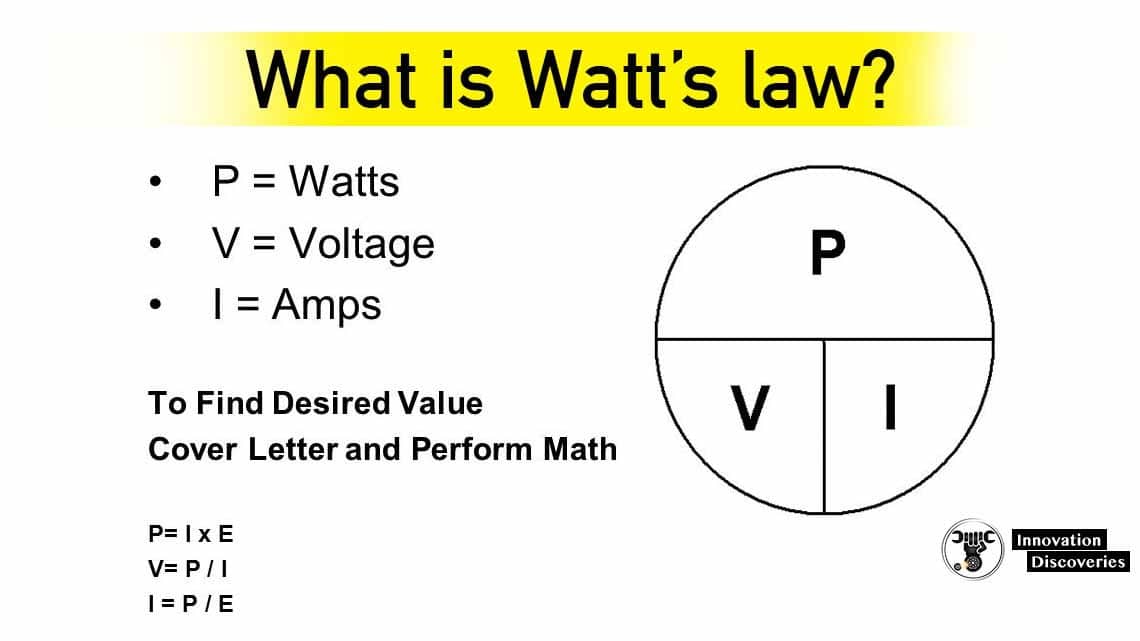
Watt’s law defines the relationship between power, voltage, and current and states that the power in a circuit is a product of the voltage and the current.
Watt ‘s law has many practical applications, and the formula for measuring Watt ‘s Law is P = IV.
You may use Watt ‘s law to calculate the voltage, power, ampere, and resistance.
Watt’s law can be combined with Ohm’s law to get many useful formulas including P=I2R and P=V2/R.
In the study of electronics, many laws and theories exist. These laws enable us to understand the workings of electric circuits and components.
One such law is Watt’s law. Watt ‘s law takes its name from James Watt, a Scottish chemist, and engineer. It defines the relationship between power, voltage, and current.
This law states that the power in a circuit is a product of voltage and current.
We’ll cover Watt ‘s law, its theory, implementations, and other related concepts in this article.
Important inputs in the definition of Watt’s law
In order for us to fully understand Watt’s law, we need to first discuss the parameters used in defining it which are:
Voltage
Voltage (V) is the electrical potential difference between two points in an electric circuit. Any difference in electrical potential causes electrons to flow from a point of higher potential to a point of lower potential. Volt is the unit of voltage (V).
Current
The current (I) is the amount of electric charge flowing through a point in a circuit at any given time. Its unit is the ampere, or “amps” (A). Current can only flow when there is a difference in electrical potential.
Resistance
Resistance (R) is the opposition to the flow of current. It is a measure of an electrical component’s ability to resist the flow of electrical current. The unit of measure is ohms (Ω).
Ohm’s law specifies the relationship between current, resistance, and voltage. This law states that the current passing through a conductor is directly proportional to its voltage, i.e., I=V/R
Power
Power (P) is a measure of the quantity of work a circuit can do, or a component can consume per unit time. Simply put, it is the amount of electrical energy transferred per unit time. The unit of power is joule per second (J/sec) also known as watts (W).
Watt’s law formula
The formula for Watt’s law is: P=IV
Where:
I = current
P = power
V = voltage
People often ask; what is the difference between Watt’s law and Ohm’s law? While Ohm’s law defines the relationship between resistance, voltage, and current in a circuit; Watt’s law defines the relationship between power, voltage, and current.
However, you can combine these laws to get useful formulas. According to Ohm’s law, I=V/R and V=IR. Substituting these into Watt’s formula, we get:
P=IxIR=I2R and P=VxV/R=V2/R
These formulas can also be used to derive several other formulas.
You can carry out most calculations involving Watt’s formula manually. However, you can also use an online Watt’s law calculator.
Applications of Watt’s law
The following are some of the applications of Watt’s law formula:
If you have a power source, you can use this formula to calculate the actual power the source can generate. You can also use it to calculate the power requirement of a component. Given the current and the voltage of the source, all you need to do is multiply the values.
You can calculate the power requirement of a building using Watt’s formula. When designing the wiring of a building, it is necessary to estimate its total power requirement. You can then use this information to determine the suitable wire sizes for the building.
You can also estimate its electricity costs. The power requirement of a building is achieved by calculating the individual power rating of every electrical appliance or component the building will have and adding them up.
When you know the power and the voltage of an electrical component, you may calculate its current, using Watt’s formula (I=P/V). The same also goes for voltage when only current and power are known (V=P/I).
The formulas derived from the combination of Watt’s law and Ohm’s law can be used to calculate the electrical resistance of a component. For example, if we have an electric bulb installed in a room, the electrical resistance of the bulb can be calculated using P=V2R i.e. R=P/V2.
Assuming the voltage supplied to that room is x volts, and the bulb is rated at y watts, then the resistance, R=x/y2.