Introduction
A dimension is a measure of a physical quantity (without numerical values), while a unit is a way to assign a number to that dimension.
Example:
Length is a dimension that is measured in units such as feet(ft), centimeter(cm), meter, kilometer(km).
kg , mol , cd , K , A , m , s
Primary dimensions and SI units
| Dimensions | Symbol | SI unit |
|---|---|---|
| Mass | M | kg (kilogram) |
| Length | L | m (meter) |
| Time | T | s (second) |
| Temperature | θ | K (Kelvin) |
| Electric Current | I | A (Ampere) |
| Amount of Light | C | Cd (candela) |
| Amount of Matter | N | M (mole) |
All non-primary dimensions can be formed by some combination of the seven primary dimensions.
Dimensions of the non-primary quantities
| Quantity | Units | Dimensions |
|---|---|---|
| Area | m2 | L2 |
| Volume | m3 | L3 |
| Velocity | m/s | LT -1 |
| Acceleration | m/s2 | LT -2 |
| Force | neweton (N) | MLT -2 |
| Work (or energy) | joule (J) | ML2T -2 |
| Power | watt (W) | ML2T -3 |
| Pressure | N/m2 | ML-1T -2 |
| Density | kg/m3 | ML -3 |
| Frequency | hertz (Hz) | T -1 |
Dimensional Analysis
Dimensional Analysis is the algebraic conversion of one measurement unit to another using conversion factors.
Why do we want to do this?
When making scientific calculations, it is necessary for the numbers used to be dimensionally consistent.
Consider Newton’s second law
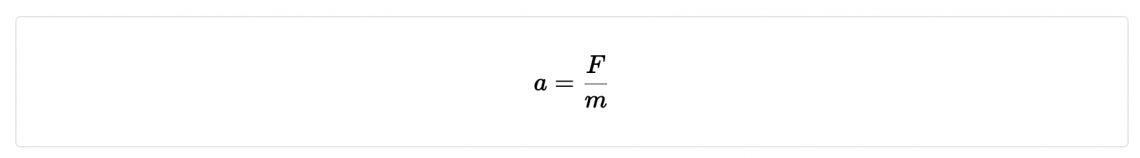
- What is the unit label for acceleration?
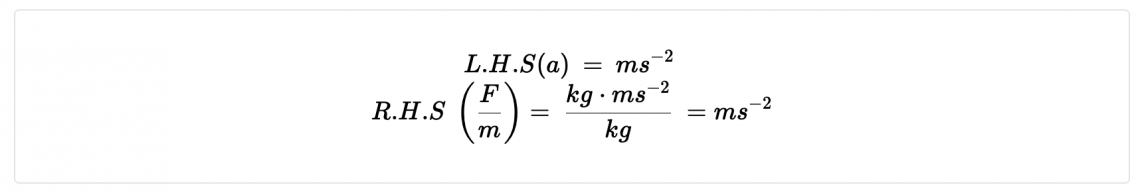
- If Force is measured in kg m/s2, what units must mass be measured in?
❖ If a mass is given in pounds, the measurement must be converted to kilograms in order for the calculation to be dimensionally consistent.
Dimensionless Quantities
- Some quantities are said to be dimensionless.
- The ratio of one mass m1 to another mass m2 is dimensionless:
Dimension of the fraction,
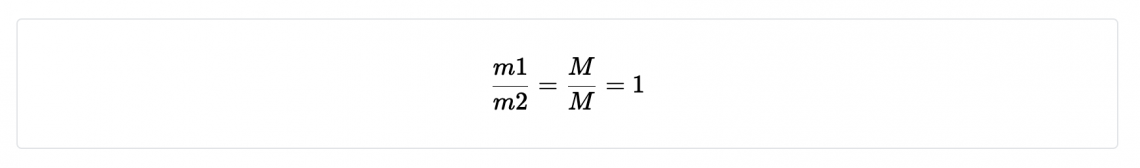
The dimensions have cancelled and a result is a number.
- Constants are dimensionless.
- The following quantities are important cases of dimensionless quantities.
Ex: Trigonometric functions, Logarithms, exponential numbers)
Summary…
When it comes to equations the dimensions of the equation must be the same on both sides.
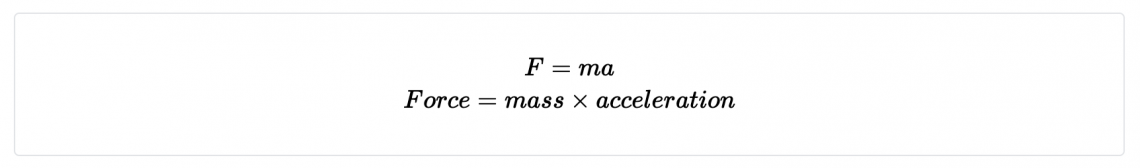
Like this most equations are being equal to both sides.
Velocity ⟶ v = m/s-1 ⟶ LT -1 ⎬ Dimensions
Acceleration ⟶ a = m/s-2 ⟶ LT -2 ⎬ Dimensions
Example 01
Q) Obtain the fundamental dimensions of,
- Velocity (units m/s)
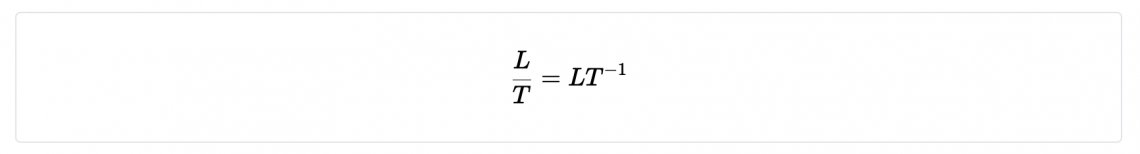
- Acceleration ( units m/s2)
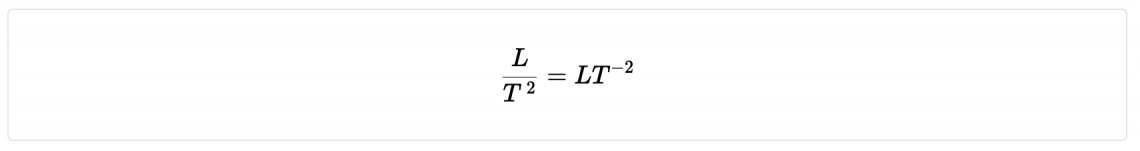
- Force ( mass x acceleration )
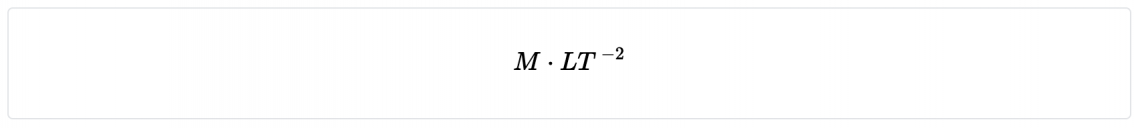
Worked Examples
- Bernoulli’s equation is given by
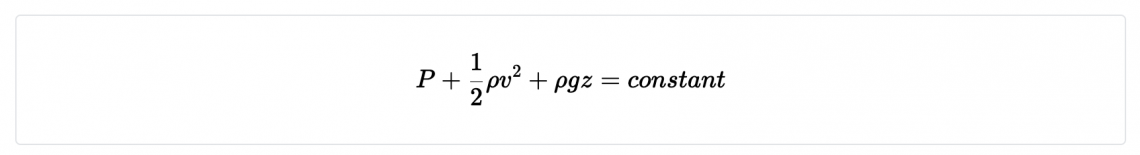
Where P = pressure, ρ=density, v=velocity, z=height, g= acceleration due to gravity. Find the dimensions of the constant.

2. The period T of a pendulum of length l is given by,

Derive equations using dimensional analysis
Example:
- Consider the oscillation of a simple pendulum, the period T may depend on mass, length, and acceleration due to gravity. If T α Lx × My × gz , derive an equation for the period T. Consider the value of the constant is 1.
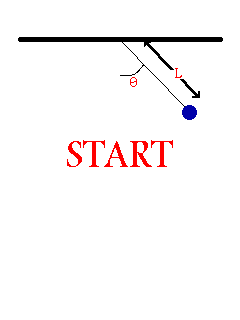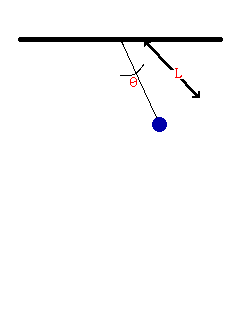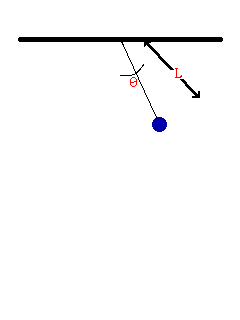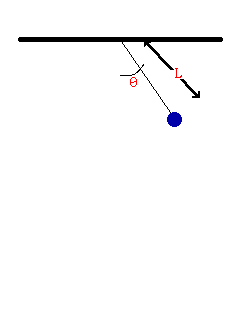
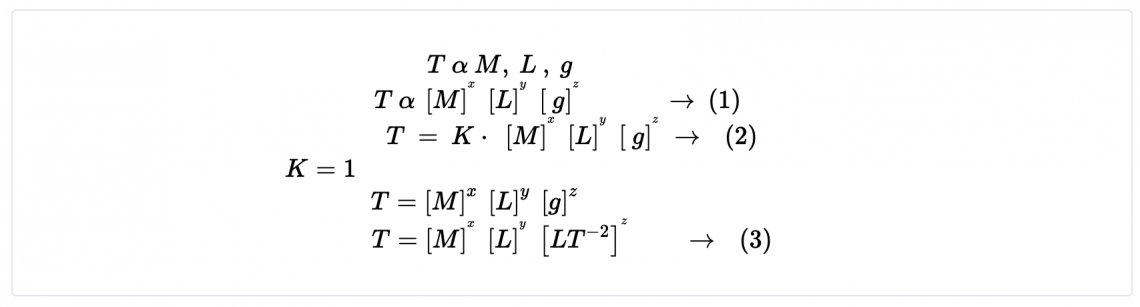
To be dimentionally consistent, the dimensions of the both sides should be equal. Therfore,

Limitations of Dimensional Analysis
- Dimensional analysis only checks the units.
- Numeric factors have no units and can’t be tested.
- Dimension analysis can not be used to derive the relation involving trigonometrical and exponential functions.
- It doesn’t indicate whether a physical quantity is a scalar or vector.
Something to know…
Units for Radiation:
The following units are used in special technologies or disciplines.
Since most people are not familiar with them, they are explained in more detail here.
Becquerel
The SI unit for radioactivity symbol (B), which is 1 disintegration per second (dps). 1 Ci = 3.7e10 B.
Curie (Ci)
A unit of radioactivity originally based on the disintegration rate of 1 g of radium.
Now a Curie is the quantity of radioactive material that has a disintegration rate of 3.700e10 per second (B). 1 mCi = 1e-3 Ci; 1 microCi = 1e-6 Ci; 1 MCi = 1e6 Ci.
Gray and Rad
Radiation dose units. The gray (Gy) is an SI unit for the absorption of 1 J radiation energy by one kg of material.
The rad was a popular unit, which is the absorption of 100 erg of radiation energy by one gram, (1 Gy = 100 rad).
Roentgen (R)
A unit for the measure of X-ray and gamma-ray exposure. 1 R = 93 erg per g (1 R = 0.93 rad for X-rays or gamma rays whose energy is above 50 keV).
The unit erg is for energy, 1 J = 10,000,000 erg.
Review Questions
1. What is the SI unit and symbol for force?
Newton (N), he defined force
One N is the gravitational pull of 98 g mass
2. What is the SI unit and symbol for pressure?
Pascal (Pa), who studied effect of pressure on fluid
1 atm = 101325 Pa = 101.3 kPa
3. What physical quantity uses the unit Joule?
Joule (J) is an energy unit
1 J = 1 N m = 10e7 ergs
4. Which is the SI unit for temperature?
Kelvin (K)
1C is the same as 273.15 K
5. What is the SI unit for measuring the amount of substance?
mole (mol), derived from Latin, meaning mass
one mole has 6.023e23 atoms or molecules
6. What are the symbols for the seven basic SI units?
m, kg, s, A, K, cd, mol
m, k, s, current, temperature, luminous, mole
7. What is the unit M used for?
M stands for mol/L, a concentration unit
8. What is the unit A used for?
1 C/s, for an electric current
9. What is the power consumption if the current is 1 A from a source of 10 V?
10 C/s V (J/s = watt)
watt is the unit for power
10. What is the SI unit for measuring radioactivity?
Becquerel (B), he discovered radioactivity
1 Ci = 3.7e10 B
Stay Tuned – Next lesson ➟ Arithmetic Progression, Geometric Progression and Trigonometric Functions
Read More:
Visit Forum
Visit Our Friendly Website