An assistant professor in Australia’s New South Wales Sydney Uni,
Has come up with a new technique for A Quicker Way Of Multiplying Huge Numbers in The conjunction is It is report that more efficient than long increase.
Associate Professor David Harvey says,
Specialized, We highlighted a 1971 theorem of shortage and stress about,
The difficulty of the integer Propagation Two German synonyms have created the Shortage – Strain algorithm.

It was the fastest method of doubling from 1971 through 2007. A faster method was developed back in 2007, but it is rarely used today.
Harvey says that Shortage and Stresses did predict that an algorithm, Multiplying n-digit numbers by Making use of n* log(n) basic operations should exist. His paper is the very first proof that it does indeed exist. Harvey chose the example of 314 multiplied by 150.
Most of the people reply to multiplying each individual number together and then adding up the sums;
9 is multiplied by 4, 1, and 3; then 5 gets multiplied by 4, 1, and 3, and so on. The result ends with 9 digit-by-digit products.
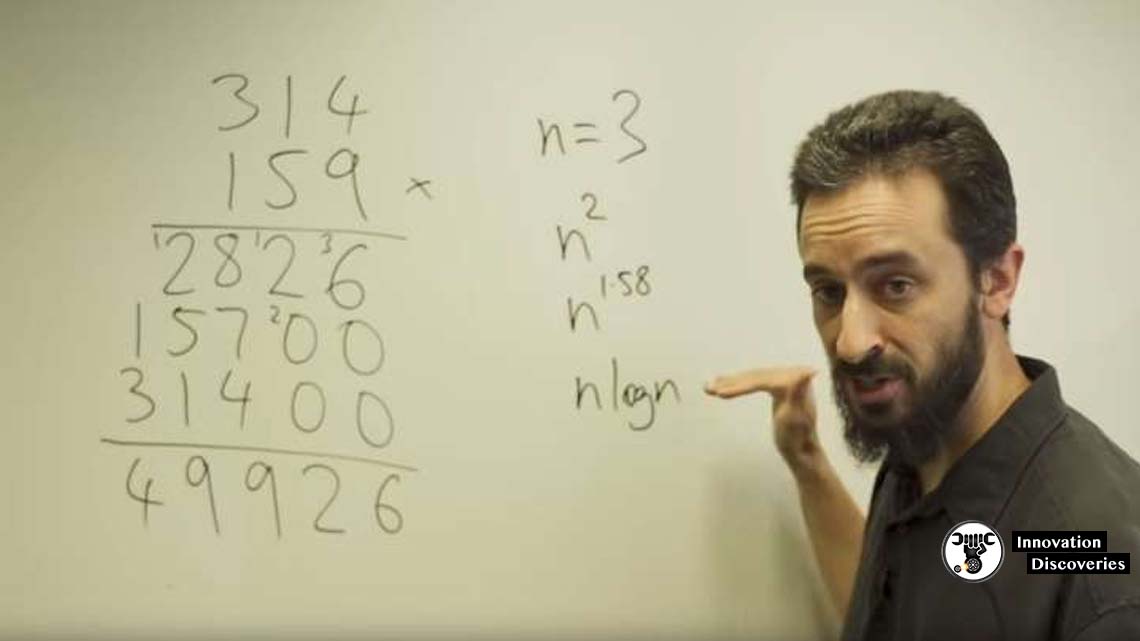
This method is referred to as n2 or n squared since one must multiply n by n a number of times. It yields the right answer, but Shortage and Stresses came with a quicker method. It was able to step away from n2 and into something smaller.
However, the form of n*log(n) did present a problem. The Schönhage-Strassen method is incredibly fast, nonetheless, as per Professor David Harvey.
A device using the squared method would need months to complete the calculation too, multiply two numbers with a billion digits.
On the other hand, using the Schönhage-Strassen method, the computer could do it in 30 seconds.
However, If numbers keep on going up into trillions and beyond,
The algorithm that has been developed by, Harvey and collaborator “Jori’s van der Ho even at Ecol Polytechnics in France; can solve the problems much quicker than the 1971 Schönhage-Strassen algorithm.
Harvey said, ‘It means you can do all sorts of arithmetic more efficiently, for example, division, and square roots.
You could also calculate the digits of pi more efficiently than before. It even has applications to problems involving huge prime numbers. People have been hunting for such an algorithm for almost 50 years.
Quicker Way Of Multiplying Huge Numbers
Also Read – Using Technology To Advance Your Career

